Quite recently, I started dabbling in Recommender Systems. My interest was piqued as a result of the pervasiveness of these systems in major technology platforms. Think of any site you use which offers suggestions to you based on your past activity: Amazon recommends books similar to ones you have liked and purchased; Netflix recommends movies similar to ones you have already enjoyed watching; Instagram’s explore feature curates images analogous to ones you have interacted with; the list goes on. Underlying these recommender systems is the basic idea that if a user likes a kind of item, we can recommend similar items to them which they haven’t yet encountered.
Recommender systems are a subclass of Information Filtering Systems. IFSs filter a stream of data using some dynamic logic to ensure that data which the user encounters is relevant to them, based on the user’s characteristics or preferences. Currently, there are three major types of recommender systems:
- Collaborative Filtering Systems
- Content-Based Filtering Systems
- Hybrid Systems
In this note, I chose to explore Collaborative Filtering Systems.
Collaborative Filtering is a method of filtering information to be presented to a user by drawing on insights extracted from different sources. Some CF techniques could make recommendations to a user based on information drawn from other user’s preferences. Instagram for instance, uses collaborative filtering to draw on accounts you follow, and use the preferences of those user accounts to recommend images in your explore page. Collaborative Filtering techniques assume that if two users share similar preferences on a bunch of subjects, then they are very likely to share preferences on other subjects. Pretty cool huh? Here’s what it looks like:
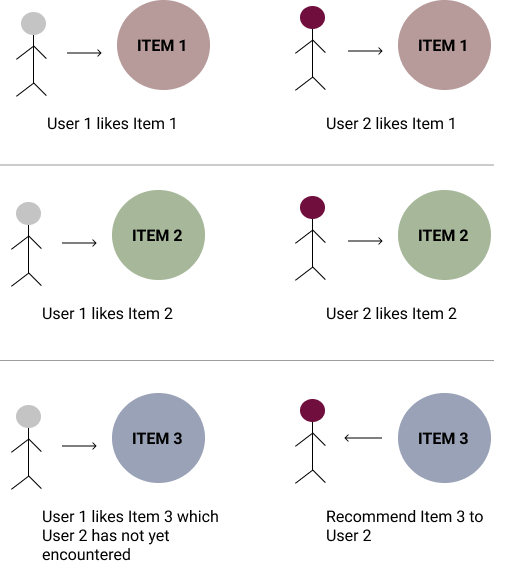
Steps to Collaborative Filtering
- Gather information on user’s preferences on the different items. (You will need to design an efficient representation of preferences)
- System should match user preferences and identify users that are most similar in terms of preference (more on this later)
- Recommend items to user that were rated highly by other similar users
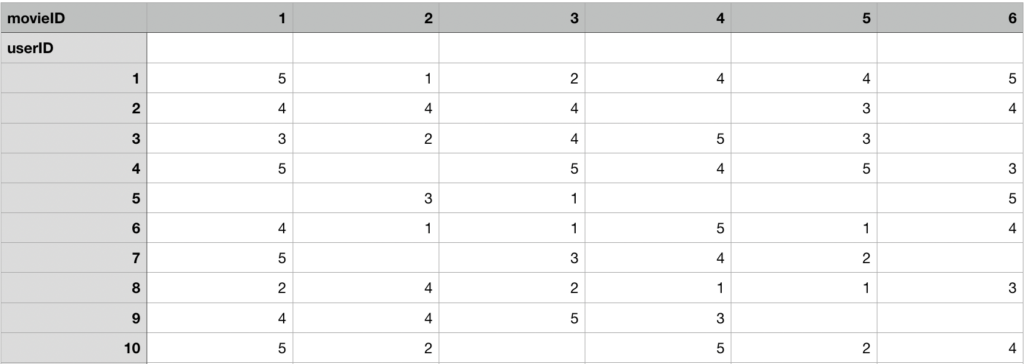
In practice, we could have a tabular matrix comprising users on the y-axis and items on the x-axis. Each row instance is a vector of the user’s rating for each item. Such a vector space is bound to have a very high number of dimensions. This is because we have created a new dimension for each item that can be rated by users. In a previous note, I delved into the Euclidean Distance algorithm for evaluating the distance between two vectors. For very high dimensional spaces, Euclid’s algorithm can fall short, because the differences in distance among vectors are somewhat negligible. We will need a more appropriate method for evaluating similarity.
One method that can work is the Cosine Similarity method. Cosine Similarity of two vectors evaluates how much the vectors are in alignment. The method is more interested in vector alignment as opposed to magnitude of distance. So that means two vectors that are very closely aligned will have a small angle between them which will give them a cosine similarity value closer to 1. The value ranges from -1 to +1 with cos(0) = 1 for perfectly similar orientation, cos(90) = 0 for perpendicular orientation, cos (180) = -1 for perfectly opposite orientation.
![]()
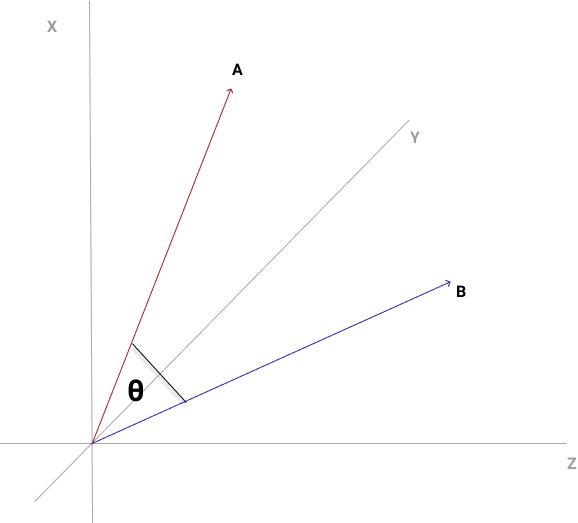
With our users organised as vectors, we can evaluate cosine similarity among users and identify the N most similar users to a user U, in terms of item preferences (ratings). For those items not yet encountered by User U, we can employ the ratings of the N most similar users and apply an average on those ratings to result in a ‘pseudo-rating’ for User U for that item. We then recommend the items with the highest ratings to User U. Using the movie recommender problem as an example, let’s define an elaborate algorithm for employing collaborative filtering.
- Organise a matrix of user ratings for movies. Each row instance is a vector of user’s ratings per movie. Each column belongs to a movie.
We assume a rating scale of 1-5. With 5 meaning the user really loved the movie. - When a user rates a movie, insert the actual rating value in the matrix.
- For a user (Henry) to whom we wish to recommend movies, compute cosine similarity between Henry’s ratings vector and every other user’s ratings vector
- Filter the most N similar users to Henry
- For each of the movies Henry has not yet watched, compute the average of the ratings from the N most similar users and set that value as Henry’s pseudo rating.
- Recommend movies with the highest pseudo-ratings to Henry.
Disadvantages of Collaborative Filtering.
- We cannot make proper recommendations until a substantial number of users have made ratings.
- System is not reliable with few users on the system
There’s another way to apply this Collaborative Filtering, where we organise our ratings matrix to have movies on the vertical axis, and users on the horizontal axis. Something like this:
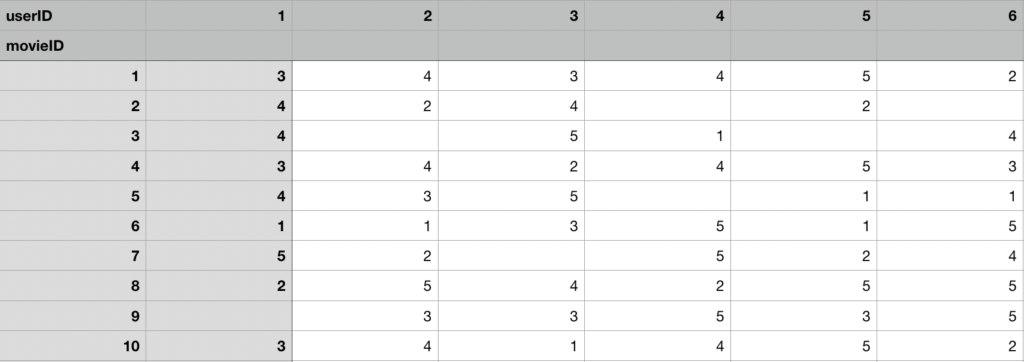
What this means is we now have our rows as movie vectors, with each vector comprising all user ratings for that movie. Using the idea of Collaborative Filtering, we can assume that when two movies have very similar user ratings, they will be more closely aligned in the vector space by cosine similarity. With this knowledge, I was able to assemble some code to parse two CSV files from movielens archive: movies.csv containing the movie data, ratings.csv containing user ratings. The goal is to build a matrix of movie vectors from the inputted data samples. The matrix which is really a scipy sparse matrix will be used to train a KNN model from which we will make our recommendations.
I also went ahead to utilise fuzzy search algorithm to allow us input a search query which will be run against the movie titles. Then I select the first search result and use it to query the KNN model for the nearest neighbours.
The last 2 paragraphs mention a few concepts that will need to be expatiated.
To understand a Scipy Sparse Matrix, first we need to appreciate why it exists. As you may know, a matrix is a 2 dimensional array of items usually denoted m by n, where m is the number of rows and n is the number of columns. When working with matrices for real world problem solving, more often than not, we encounter sparse matrices; ie matrices with A LOT of zero values. In fact, these sparse matrices have so many zero values, it becomes computationally inefficient to hold these values in memory as though they were part of a dense matrix. Hence, Scipy Sparse Matrices allow us efficiently represent 2Dimensional arrays in memory.
Fuzzy Search is an algorithm that employs a fairly loose approach to string matching. As opposed to regular expressions, or substring matching algorithms; Fuzzy search is less rigid and can match misspelled words or even words that appear out of order. I rely on the fuzzywuzzy package for implementing fuzzy search. Fuzzy search is very similar to a more popular algorithm: Levenshtein distance though it appears to be more powerful.
Another thing I tried to do was restrict the number of movies involved in the recommendation process to those movies that received a sufficient number of recommendations by users. Why this is necessary is to avoid unpopular movies clogging our recommendation process; and further prune our sparse matrix so it only has most relevant data.
Here’s what the code looks like:
import pandas as pd
from sklearn.neighbors import NearestNeighbors
from scipy.sparse import csr_matrix
from fuzzywuzzy import fuzz
class DataFrameReader:
"""
Class reads the movie and ratings files and organizes
them into Pandas DataFrames.
"""
def __init__(self, movies_path, ratings_path):
self.movies_path = movies_path
self.ratings_path = ratings_path
def load_data(self):
movies_df = pd.read_csv(
self.movies_path, usecols=['movieId', 'title'],
dtype={'movieId': 'int', 'title': 'str'}
)
ratings_df = pd.read_csv(
self.ratings_path, usecols=['userId', 'movieId',
'rating'],
dtype={'userId': 'int', 'movieId': 'int', 'rating':
'float'}
)
return movies_df, ratings_df
class MovieMatrixBuilder:
"""
Builds a Scipy Sparse Matrix holding ratings by users on most rated movies
"""
def __init__(self, movie_ratings_threshold):
self.movie_ratings_threshold = movie_ratings_threshold
def build_knn_matrix(self, movies_df, ratings_df):
filtered_movies = ratings_df[
self.get_filtered_movies(ratings_df)
]
movies_matrix = filtered_movies.pivot(
index='movieId', columns='userId', values='rating'
).fillna(0)
sparse_movies_matrix = csr_matrix(movies_matrix.values)
return sparse_movies_matrix
def get_filtered_movies(self, ratings_df):
"""
filters movies by the supplied threshold which is
applied to the count of ratings made on each movie
"""
movies_df_count = pd.DataFrame(
ratings_df.groupby('movieId').size(),
columns=['count']
)
most_rated_movies = movies_df_count.query(
'count >= @self.movie_ratings_threshold'
).index
return ratings_df.movieId.isin(most_rated_movies).values
class FuzzyWuzzyMatcher:
def __init__(self, ratio_threshold):
self.ratio_threshold = ratio_threshold
def fuzzy_search(self, movie, movie_map):
matching_items = []
for index, title in movie_map.items():
fuzz_ratio = fuzz.ratio(title.lower(), movie.lower())
if (fuzz_ratio >= self.ratio_threshold):
matching_items.append((title, index))
return matching_items
class MovieRecommender:
def __init__(self, n_neighbors, movies_path, ratings_path,
movie_ratings_threshold):
self.n_neighbors = n_neighbors
data_reader = DataFrameReader(movies_path, ratings_path)
self.movies_df, self.ratings_df = data_reader.load_data()
self.matrix_builder = MovieMatrixBuilder(
movie_ratings_threshold
)
def prepare_model(self):
self.sparse_matrix = self.matrix_builder.build_knn_matrix(
self.movies_df, self.ratings_df)
self.movie_map = {
index: row.title for index, row in
self.movies_df.set_index('movieId').iterrows()
}
self.model = NearestNeighbors(
n_neighbors=self.n_neighbors,
metric='cosine',
algorithm='brute',
n_jobs=-1
)
self.model.fit(self.sparse_matrix)
def recommend(self, movie_query, search_threshold):
matcher = FuzzyWuzzyMatcher(search_threshold)
search_results = matcher.fuzzy_search(
movie_query, self.movie_map
)
print(f'Search Results: {search_results}')
if not search_results:
print('No Results matching Search Query.')
else:
movieIndex = search_results[0][1]
distances, indices = self.model.kneighbors(
self.sparse_matrix[movieIndex]
)
return [
[self.movie_map.get(key) for key in indexRow]
for indexRow in indices
]
# read relevant parameters from user input
movies_path = input('Path to Movies CSV: ')
ratings_path = input('Path to User Ratings CSV: ')
search_threshold = input('Fuzzy Search Threshold: ')
neighbors_count = input('Number of Neighbors: ')
movie_ratings_threshold = input('Movie Ratings Threshold: ')
# apply unpacking operator to initialize movie
# recommender with named arguments
recommender = MovieRecommender(
**{
'n_neighbors': int(neighbors_count),
'movies_path': movies_path,
'ratings_path': ratings_path,
'movie_ratings_threshold': int(movie_ratings_threshold)
}
)
recommender.prepare_model()
movie_query = input('Movie Name: ')
recommender.recommend(movie_query, int(search_threshold))
Here’s a link to the file on github: movie_recommender_main.ipynb
Wrapping Up
What I implemented in this note is far from a production grade recommender system. Although it introduces the basic concepts of Collaborative Filtering. Real world systems are usually Hybrid; employing a mix of Collaborative, Content Based filtering, and even more advanced methods. It would be great to explore these in subsequent notes.